Discretización
Discretización
La discretización
de datos consiste en aproximar un continuo, o un conjunto
discreto muy grande, por un conjunto discreto de tamaño
limitado. El tamaño limitado permite el almacenamiento digital
y procesamiento de información.
Discretización
de mapas
Algunas
características que queremos representar en mapas varían de
forma continua (e.g. elevación, temperatura, presión
atmosféricas, vegetación natural o tipo de suelo). Para poder
almacenar datos espacialmente, tenemos que asignar valores
discretos a estas entidades. Para atacar al problema de la
variación continua podemos utilizar varias técnicas:
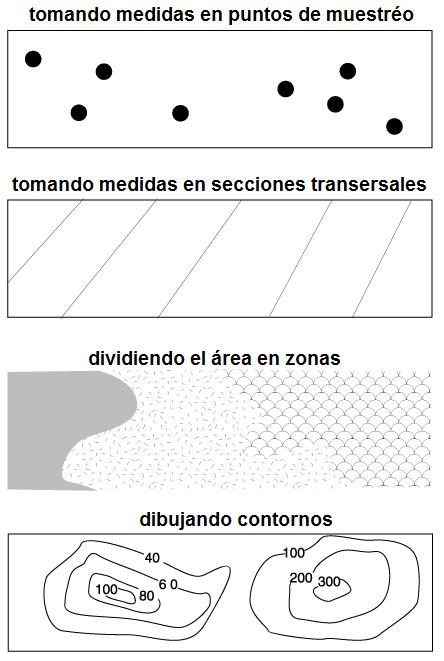
- Realización de mediciones en puntos de muestreo
como estaciones meteorológicas, situando contadores de
tráfico en las intersecciones de calles.
- Podemos tomar secciones transversales a
intervalos e interpolar entre los sitios de muestreo. Esto
se utiliza en el muestreo geológico.
- Dividiendo un área en zonas y suponiendo que la
variable es constante dentro de cada zona. Así es como
funciona el mapeo de suelos. También es el principio detrás
de la enumeración en censos.
- Dibujando contornos. Esto se hace para elevaciones de cartografía topográfica.
Características de la
discretización
- Cada uno de
estos métodos crea objetos discretos.
- Los
objetos en cada caso son puntos, líneas o áreas.
- La captura
es solo una aproximación de sólo una parte de la variación
real.
Problemas con discretización
El propósito de la discretización es simplificar los datos:
- Tomado una muestra en un punto o sección transversal. Esto hace perder variación entre puntos o elementos que no están en la sección transversal.
- Creando zonas donde no hay ninguna variación dentro de las zonas, causando una variación repentina.
- Creando contornos donde cada uno refleja un valor fijo y por lo tanto no se muestran las variaciones entre los contornos.
Discretización de imágenes
Un ejemplo relativamente simple es la discretización de una imagen bidimensional rectangular en tonos de gris. La imagen viene dada por una función
La forma más sencilla para discretizar el rectángulo \(R_2\) es elegir un número \(q\) positivo y superponer sobre el rectángulo una cuadrícula de pequeños cuadrados de lado \(q\).
Por lo general, el objetivo en el diseño de una buen discretización es minimizar el " error de cuantización", i.e., minimizar la distancia entre puntos de datos \((x,y)\) y sus discretizaciones. Por ejemplo, el error de cuantificación es el valor máximo de \(|(x,y) - g (x,y)∙q|\).
[Véase, por ejemplo: J. H. Conway, N.J.A. Sloane, Sphere packings, lattices and groups, Springer-Verlag (1998).
Discretización de contornos
La discretización es en general un proceso complejo. Para ilustrar este proceso vamos a simplificar y considerar la discretización de contornos. Un contorno puede ser discretizado tomando un conjunto de puntos en el contorno que se unen con segmentos. Por ejemplo un círculo lo podemos aproximar convenientemente con polígonos regulares. Al aumentar el número de lados la aproximación es más fidedigna.
En las escenas del desarrollo dos y tres exploramos primero la discretización de segmentos rectos con cuadrados pequeños y esto lo aplicamos a la discretización de figuras más complejas.
Otros ejemplos de discretización
Cuando los datos o el procesamiento de estos tiene alguna incertidumbre, su discretización puede producir resultados significativamente diferentes. Por ejemplo, en ciertos esquemas de contraseña gráficos, una ligera incertidumbre en el proceso de discretización puede producir una contraseña diferente. Existen métodos de discretización que son tolerantes a las incertidumbres usando un error de distancia \(r\), que se puede ajustar a las aplicaciones. Esto permite implementar esquemas de contraseña gráficos muy flexibles y de marcas de agua digitales.
Otra aplicación importante de la discretización es en el aprendizaje automático, que requiere la concepción y el desarrollo de algoritmos que permiten a las computadoras evolucionar comportamientos basados en datos empíricos. El aprendizaje automático, incluye la minería de datos y el descubrimiento de conocimientos. Dado que el objetivo es aprender a partir de datos empíricos obtenidos en el mundo real, la discretización se encuentra en todo proceso de aprendizaje automático de objetos continuos. Estas disciplinas se han desarrollado rápidamente en los últimos años y se está convirtiendo en un tema enorme no sólo en las comunidades de investigación, pero también en las empresas e industrias.
Créditos
| Diseño del contenido | Víctor Manuel Amezcua Raz (LITE) |
| Diseño funcional | Víctor Manuel Amezcua Raz (LITE) |
| Programación | Víctor Manuel Amezcua Raz (LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

