Comentarios sobre máquinas de estado finito
Autómatas de estado finito
Hemos visto un ejemplo de máquinas de estado finito que
producen salidas usadas para controlar otros dispositivos o
para generar una respuesta que corresponde a la sucesión de
entradas que recibe la máquina.
A pesar de su aparente simplicidad, la MEF que se
muestra en el diagrama, implementa un bit de memoria.
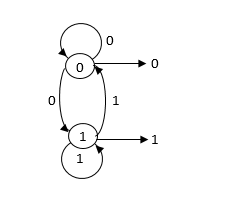
Cuando recibe \(0\) como entrada, si la MEF está en el estado \(0\), permanece en ese estado y si está en el estado \(1\) cambia al estado \(0\) lo que significa que este valor es guardado por la MEF en el estado \(0\). “Leyendo” el estado de la MEF nos dice que hay un \(0\) guardado. Similarmente, cuando recibe \(1\) como entrada, si la MEF está en el estado \(1\), permanece en ese estado y si está en el estado \(0\) cambia al estado \(1\) lo que significa que este valor es guardado por la MEF en el estado \(1\). “Leyendo” el estado de la MEF nos dice que hay un \(1\) guardado.
Otro tipo de MEF, llamadas autómatas de estado finito, usadas para reconocer lenguajes, tiene un subconjunto de estados llamado estados finales. Estas máquinas no tienen una función de salida. El resultado de su ejecución está indicado por la clase de estado en el que la ejecución termina. Solo hay dos clases de estados, los estados finales y los no finales. Cuando la máquina recibe como entrada a una posible cadena del lenguaje y la máquina va del estado inicial a uno de los estados finales, decimos que la cadena ha sido reconocida o aceptada por la máquina. El lenguaje reconocido por la máquina consiste de la colección de todas las cadenas aceptadas por el lenguaje. Si la máquina va del estado inicial a uno de los estados no finales, decimos que la cadena de entrada no es parte del lenguaje.
Máquinas de Turing
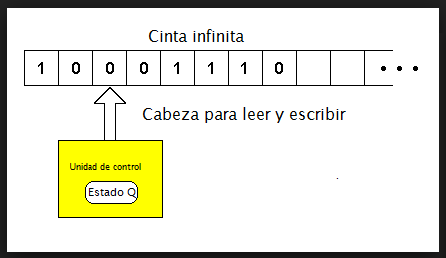
Las máquinas de estado finito se pueden generalizar. Una máquina de Turing consiste de todo lo incluido en una máquina de estado finito, junto con una cinta, que es infinita en ambas direcciones. Una máquina de Turing tiene la capacidad de leer y escribir en la cinta, y puede moverse hacia atrás y hacia adelante a lo largo de la cinta. Las máquinas de Turing pueden modelar todos los cálculos que se pueden realizar en una máquina de computación. Debido a su poder, las Máquinas de Turing son estudiadas extensamente en ciencias de la computación teórica.
En “Computation: Finite and Infinite Machines, Prentice–Hall, Inc., N.J., 1967.” Marvin Minsky dice:
El artículo de Turing ... contiene, en esencia, la invención de la computadora moderna y algunas de las técnicas de programación que la acompañan.
—Minsky (1967), p. 104
Créditos
| Diseño del contenido | Gustavo Magallanes Guijón |
| Diseño funcional | Gustavo Magallanes Guijón |
| Programación | Gustavo Magallanes Guijón |
| Asesoría de programación | Víctor Manuel Amezcua Raz (LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

