Máquinas de estado finito y máximo común divisor
Máquinas de estado finito
Una máquina de estado finito, MEF, es una abstracción matemática que nos permite modelar la computación. En esta lección vamos a usar una MEF para controlar a una unidad aritmética en el cálculo del máximo común divisor, de dos números naturales \(a\), \(b\), denotado por \(MCD(a,b)\).
Para especificar una MEF necesitamos tres conjuntos finitos, \(E\), \(Q\), \(S\); dos funciones \(T: E \times Q \rightarrow Q\), \( θ: Q \rightarrow S \); y un elemento \(q_0\) de \(Q\). Los elementos de \(E\) se llaman símbolos de entrada, los de \(Q\) estados, y los de \(S\), símbolos de salidas. La función \(T\) define transiciones de estado que dependen del elemento de entrada cuando la máquina se encuentra en un estado dado. La función \(θ\) define cual es la salida asociada a cada estado. El elemento \(q_0\) es el estado inicial con el que la máquina empieza su operación. A estas máquinas se les conoce como Moore machines.
Hay variaciones en la definición tales como considerar que la función \(θ\) dependa también de las entradas y no solo del estado en que se encuentra, i.e., \(θ: E \times Q \rightarrow S\). A estas máquina se les conoce como Mealy machines. Cada máquina de Moore es equivalente a una máquina de Mealy, mientras que una máquina de Mealy se puede convertir sólo a una máquina de Moore casi equivalente, excepto que tiene las salidas desplazadas en el tiempo.
Vamos
a considerar un ejemplo muy sencillo para mostrar la notación
gráfica que se usa para describir las
MEF. La MEF está definida por
\(Q = S = I = \lbrace 0, 1\rbrace \), la función \(T\) está dada por la tabla:
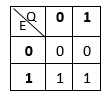
La función \( θ \) es simplemente la identidad, esto es \( θ(0) = 0 \) y \( θ(1) = 1 \)
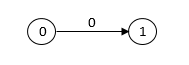
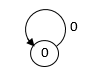
Y para denotar la transición del estado \(0\) a si mismo con la entrada \(0\) vamos a usar el diagrama de bucle:
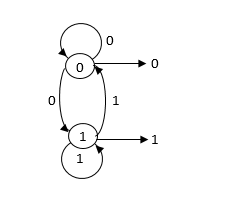
Haciendo esto para cada casilla de la tabla obtenemos el diagrama completo de la MEF:
©
Créditos
| Diseño del contenido | Gustavo Magallanes Guijón |
| Diseño funcional | Gustavo Magallanes Guijón |
| Programación | Gustavo Magallanes Guijón |
| Asesoría de programación | Víctor Manuel Amezcua Raz (LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

