¿Qué es una superficie cuadrática?
Una \(superficie \) \(cuadrática \) es la gráfica de una ecuación de segunto grado con variables \(x\), \(y\) y \(z\) en un espacio tridimensional. La forma más general de esta ecuación es \[ Ax^2+By^2+Cz^2+Dxy+Eyz+Fxz+Gx+Hy+Jz+K=0 \] donde \(A \), \(B \), \(C \), \(D \), \(E \), \(F\), \(G \), \(H \), \(J \) y \(K \) son constantes. Esta ecuación se llama precisamente Ecuación general de segundo grado, y puede simplificarse por medio de una rotación y/o una translación, de manera que la ecuación quedará como \[ Ax^2 + By^2 + Cz^2 + Dz +E= 0 \] Observa que ésta última no tiene términos cruzados, es decir los términos \(xy\), \(yz\) y \(xz\). Otro tipo de ecuación es la Ecuación canónica. Un ejemplo es la ecuación canónica de la elipsoide: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\), cuya gráfica es
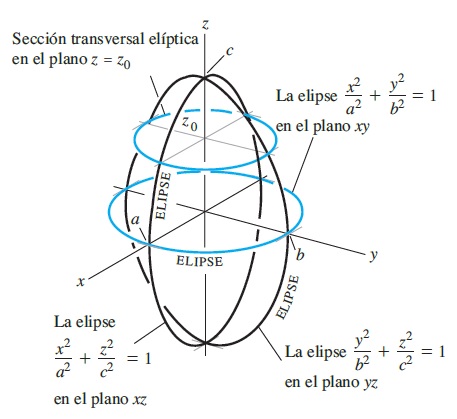
En este caso \(A=b^2c^2\), \(B=a^2c^2\), \(C=a^2b^2\), \(D=0\) y \(E=-a^2b^2c^2\), de manera que podemos pasar de una a otra.
En la sección anterior ya vimos los nombres y las gráficas de estas superficies. Estas gráficas pueden cambiar de acuerdo a cómo son y cómo cambian las constantes \(A \), \(B \), \(C \), \(D \) y \(E \), como veremos en la siguiente sección. En el siguiente video podrás ver algunos ejemplos de ecuaciones de segundo grado y su gráfica.
Créditos
| Diseño del contenido | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Diseño funcional | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Programación | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Asesoría de programación |
José Luis Abreu León (Instituto de Matemáticas, UNAM) Leticia Montserrat Vargas Rocha |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

