¿Qué es una superficie paramétrica?
Curva
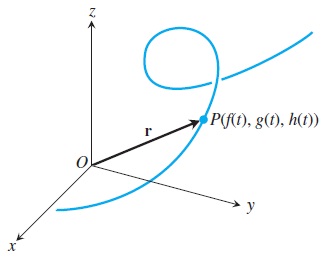
Normalmente, en un plano, vemos a una curva como la gráfica de una función expresada de manera explícita, es decir, una ecuación donde una de las variables está dada en términos de las otras dos. Sin embargo, para describir la trayectoria de una partícula como una curva en el espacio como la que se muestra en la figura, más que describirla con una expresión que relacione una de sus coordenadas en términos de las otras dos, nos conviene expresar cada una de las coordenadas de la partícula como una función del tiempo \(t \). Entonces la curva expresada de esta manera será la trayectoria de la partícula. Las ecuaciones, \(x=f(t) \), \(y=g(t) \) y \(z=h(t) \) son funciones que nos dicen cuál es la posición de la partícula en cualquier tiempo \(t \) y están definidas en un \(intervalo \) \(I \). El conjunto de puntos \( (x,y,z)=(f(t),g(t),h(t)) \) es una \(curva \) en el espacio. Las ecuaciones se llaman \(ecuaciones \) \(paramétricas \) de la curva y \(t \) es el parámetro. Las ecuaciones y el intervalo constituyen una \(parametrización \) de la curva.
Superficie
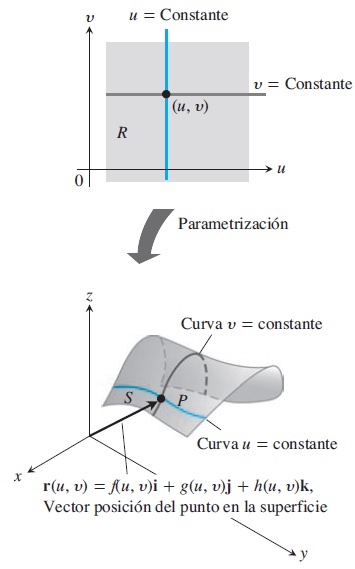
De la misma manera, podemos parametrizar una superficie expresando las coordenadas de cada uno de sus puntos como una función vectorial de dos variables. Sea \[ r(u,v)=f(u,v)i+g(u,v)j+h(u,v)k \] una función vectorial continua definida en una región \(R \) en el plano-\(uv \) y uno a uno en el interior de \(R \). El rango de \(r \) la \(superficie \) \(S \) definida por \(r \). \(r \) junto con el dominio \(R \) constituyen una \(parametrización \) de la superficie y las variables \(u \) y \(v \) son los parámetros. Observa que la ecuación anterior es el vector compuesto por las tres ecuaciones paramétricas: \[x=f(u,v), \ \ \ y=g(u,v),\ \ \ z=h(u,v). \] y que éstas nos dan la posición de un punto en la superficie. Decimos que \(S \), expresada de esta forma, es una \(superficie \) \(paramétrica. \)
Créditos
| Diseño del contenido | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Diseño funcional | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Programación | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Asesoría de programación |
José Luis Abreu León (Instituto de Matemáticas, UNAM) Leticia Montserrat Vargas Rocha |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

