¿Qué es una curva paramétrica?
Normalmente, en un plano, vemos a una curva como la gráfica de una función expresada de manera explícita, es decir, una ecuación donde una de las variables está dada en términos de las otras dos. Sin embargo, para describir la trayectoria de una partícula como una curva en el espacio como la que se muestra en la figura, más que describirla con una expresión que relacione una de sus coordenadas en términos de las otras dos, nos conviene expresar cada una de las coordenadas de la partícula como una función del tiempo \(t \). Para realizar el seguimiento de una partícula que se mueve en el espacio, se tira un vector \(r\) desde el orígen del espacio cartesiano hasta la partícula y estudiamos los cambios en \(r\).
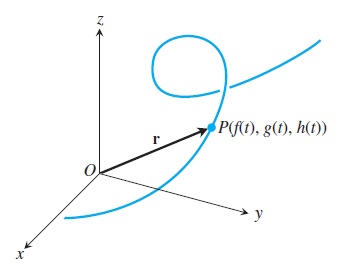
Entonces la curva expresada de esta manera será la trayectoria de la partícula. Las ecuaciones, \(x=f(t) \), \(y=g(t) \) y \(z=h(t) \) son funciones que nos dicen cuál es la posición de la partícula en cualquier tiempo \(t \) y están definidas en un \(intervalo \) \(I \). El conjunto de puntos \( (x,y,z)=(f(t),g(t),h(t)) \) es una \(curva \) en el espacio. Las ecuaciones se llaman \(ecuaciones \) \(paramétricas \) de la curva y \(t \) es el parámetro. Las ecuaciones y el intervalo constituyen una \(parametrización \) de la curva. El vector
\[\textbf{r}(t)=\overrightarrow{OP}=f(t)\textbf{i}+g(t)\textbf{j}+h(t)\textbf{k} \]
que va del orígen a la posición de la partícula \(P(f(t),g(t),h(t)) \) en el tiempo \(t \) es el \( vector\) \(de \) \(posición\) de la partícula.
Si las coordenadas de la posición de la partícula son funciones del tiempo dos veces diferenciables, entonces también \(r\) es dos veces diferenciable, y por lo tanto podemos encontrar vectores de velocidad y de aceleración de la partícula en cualquier momento mediante la diferenciación de \(r\). Y si conocemos el vector de velocidad de la partícula o de aceleración como una función continua del tiempo, y tenemos suficiente información sobre la velocidad y la posición iniciales de la partícula, tendríamos una ecuación diferencial y por lo tanto podriamos encontrar \(r\) como una función del tiempo mediante la integración (analítica o numérica). De manera que, en ambos casos, podemos describir el movimiento de la partícula.
©Créditos
| Diseño del contenido | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Diseño funcional | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Programación | Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM) |
| Asesoría de programación |
José Luis Abreu León (Instituto de Matemáticas, UNAM) Leticia Montserrat Vargas Rocha |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

